どうも、Tomatsuです。
配当割引モデルの株式価値の式(V = D / r )は暗記したのですが、意味も分からず使っています。。。
なぜ配当金を期待収益率で割れば株式価値が求められるのでしょうか?
あと成長率を考慮する場合、分母の割引率を成長率で引くのも意味不明です。。。
企業価値計算の継続価値も上記同様、式の意味が理解できていません。
このような疑問にお答えします。
配当割引モデルと継続価値の式の意味と導出法を覚える
記事を書いている私は、財務・会計関連の「知識ゼロの状態」から、中小企業診断士試験にストレート合格しました(財務・会計は84点)。
現在は会社員をやりながら、診断士受験用のテキスト本の執筆や、受験生支援ブログにて執筆活動(一発合格道場)を行っています。
効率的な勉強法には自信がありますし、結果も出してきていると言えます。
配当割引モデルと継続価値の式は導出しよう│暗記はNG

まずは配当割引モデルおよび企業の継続価値の式をみてみましょう。
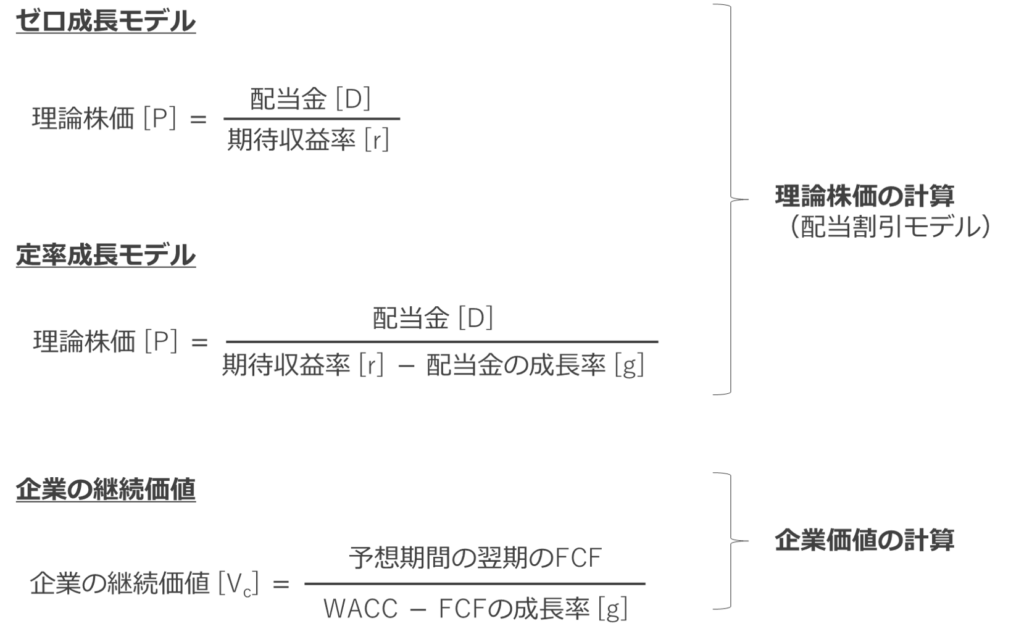
正直パニック状態ですね。。。
あるいは式自体は暗記しているけど、なんでこんな式で計算できるのか分からないという人は多いのではないでしょうか?
全て同じ理屈で導出できる(等比数列の和の公式を使う)

上記の式は全て「等比数列の和の公式」を使うことで導出できます。
トウヒスウレツノワ?なんじゃそりゃ(汗)
数学嫌いの方はアレルギー反応が出るかもしれませんが、分かりやすく解説しますので読み進めてみて下さい。
ゼロ成長モデルとは?
まずは一番簡単なゼロ成長モデルからみていきましょう。
そもそもゼロ成長モデルの本来の意味および式は下記の通りです。
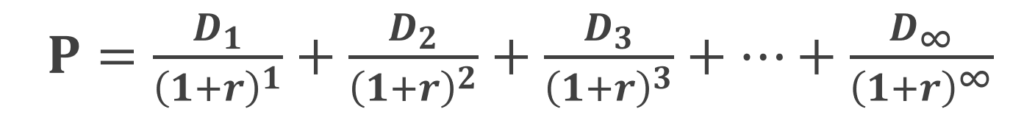
む、無限が出てきた…(汗)
3年後までであれば、現価係数で一つずつ解いていけるのですが…
そうなんです。
項が無限にありますので、一つずつ計算する訳にはいきませんよね。
そこで、高校数学で学んだ「等比数列の和の公式」という裏技を用います。
等比数列の和の公式
等比数列の和の公式とは、初項 [a]、公比 [r] の等比数列
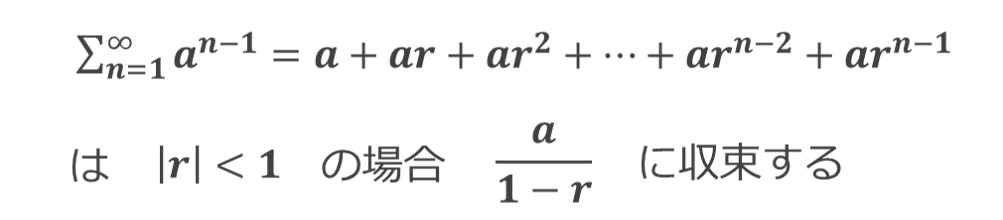
というものです。
[導出過程]
例えば、初項からn項まで足し合わせた値を次のように 「S」とし
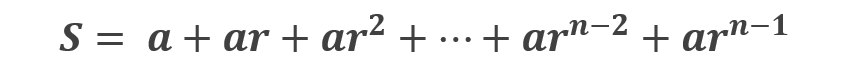
そこに公比[r]を掛けたものを次のように 「rS」 とします。
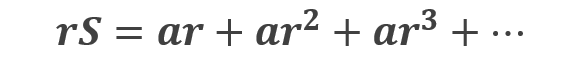
次に S-rS を計算すると

右辺は「a以外」すべて相殺されるため
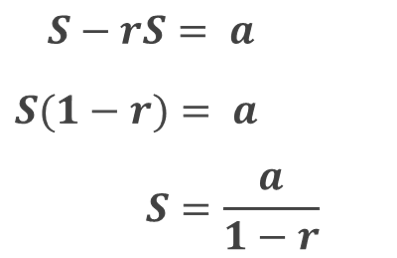
となる。
自分で鉛筆を動かしながら確認すると効果的です。
公式を使ってゼロ成長モデルを導出してみよう
つぎに、上記と同じ方法をつかってゼロ成長モデルを導出してみましょう。
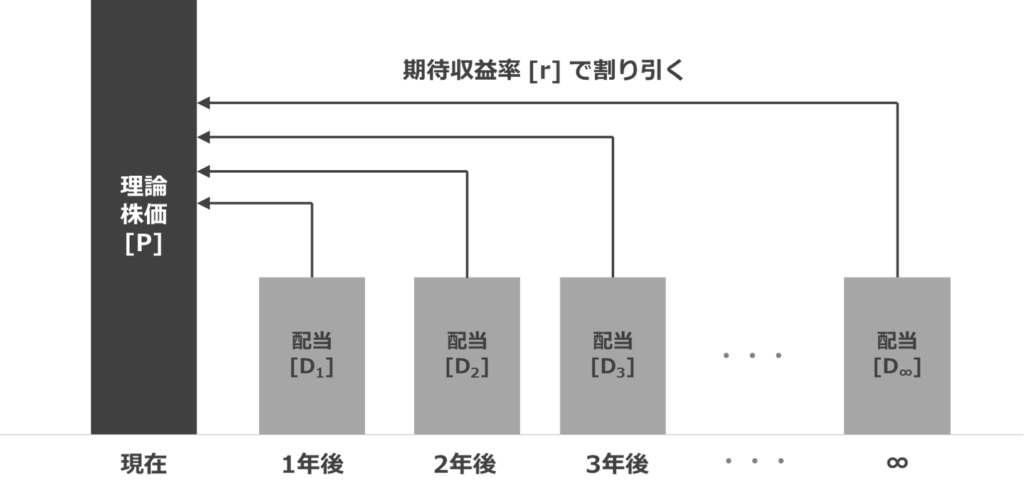
理論株価[P]は将来得られるインカムゲインを現在価値に割り引いたものの総和なので下記の通り表します。
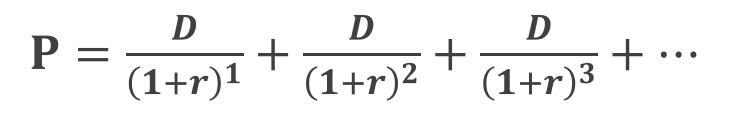
この等比数列における公比は 「 1 / ( 1 + r ) 」 であることが分かります。
つぎに 「 1 / ( 1 + r ) 」 を両辺に掛けると
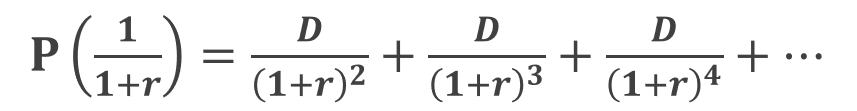
が得られます。
つぎに両式の差を取ると
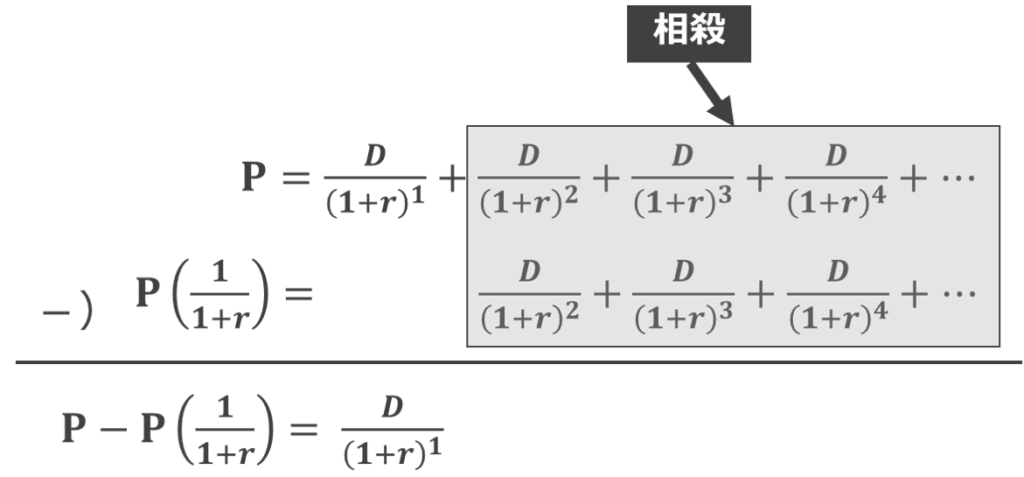
が得られ、あとは 「P」 について解いていくだけです。

成長率を考慮する場合

つぎに定率成長モデルがなぜ下記のような式になるのか?について見ていきましょう。

なぜ「分母で成長率を引く」のかが意味不明です。。。
少しだけ複雑になりますが、導出法はゼロ成長モデルの時と同じです。
早速見ていきましょう。
定率成長モデルとは?
定率成長モデルは、将来得られる配当が一定の成長率で増加していくと仮定したモデルです。
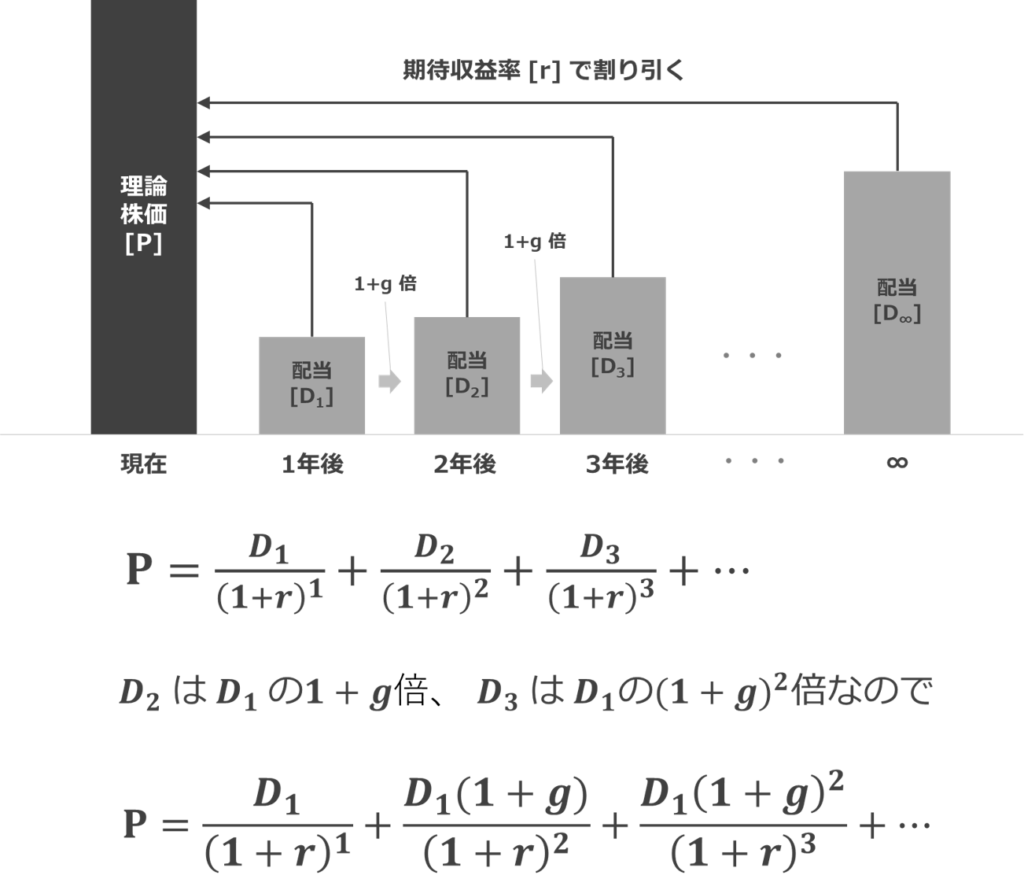
等比数列の和の公式を使う
これもゼロ成長モデルの時と同様、等比数列の和の公式を使って簡易化すれば良いのです。
[導出過程]
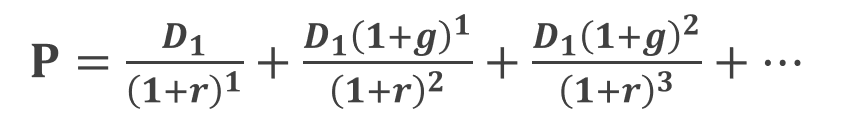
この等比数列における公比は 「 (1 + g ) / ( 1 + r ) 」 であることが分かります。
つぎに 「 (1 + g ) / ( 1 + r ) 」 を両辺に掛けると
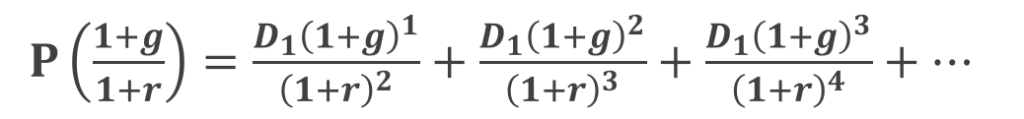
が得られます。
つぎに両式の差を取ると

が得られ、あとは「P」について解いていくだけです。
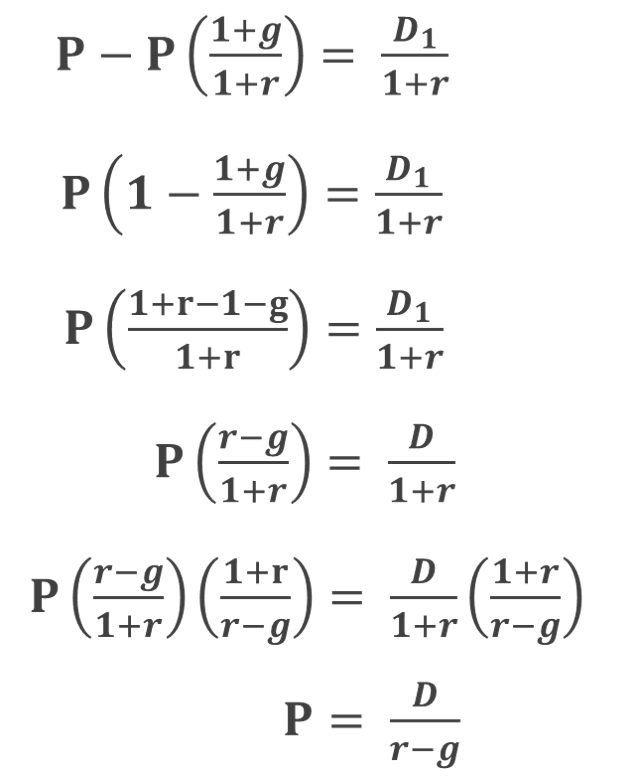
すっきりしましたね!
企業価値における継続価値計算の式も全く同じ方法で導出できます。
企業価値における継続価値計算の式も上記と完全に同じ方法で導出できます。
補足:ご質問の回答(22年12月2日)

コメント欄に下記のご質問頂きましたので、補足させていただければと思います。
色々とわかりやすい内容開示いただきありがとうございます。恐らくこちらの論点になるかと思っていますが財務会計R3年第21問の解説を数列の和を使わず棒グラフなどの直感的な形で解法を記事にしていただければと思いますので一度ご検討だけでもお願いしたいと思います。本問の解説に関してはなかなか詳細かつ丁寧な解答記載のあるモノがなく困っております。
[令和3年度の財務・会計21問]
D社の次期(第 2 期)末の予想配当は 1 株 44 円である。その後、次々期(第 3 期)末まで 1 年間の配当成長率は 10 %、それ以降の配当成長率は 2 %で一定とする。なお、自己資本コストは 10 %である。当期(第 1 期)末の理論株価として、最も適切なものはどれか。
ア 540円
イ 590円
ウ 645円
エ 649円
参照元:https://www.j-smeca.jp/attach/test/shikenmondai/1ji2021/B1ji2021.pdf
ぱっと見シンプルに見えますが、かなり複雑な問題です。
落ち着いて要件を整理すると、以下のような模式図が描けるはずです。
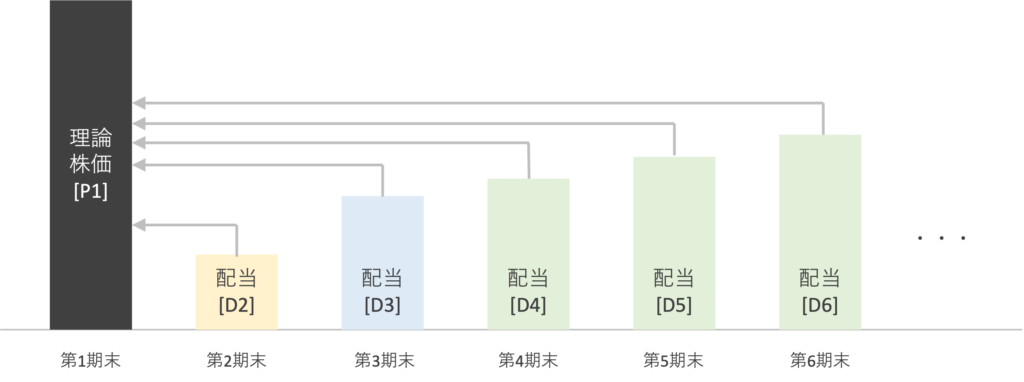
まずは問題文の要件から第2期末の予想配当[D2]が44円であることが分かります。
また、第3期末の予想配当額[D3]は10%の成長率が期待されているので、単純計算で、D3は48.4円になることが分かります。
ややこしくなるのはここからです。第4期末以降の予想配当額の成長率は10%ではなく2%となります。
一つずつ計算していけば良いのですが、時間の制約を踏まえると現実的でないので、「定率成長配当割引モデル」が使えることに着目する必要があります。
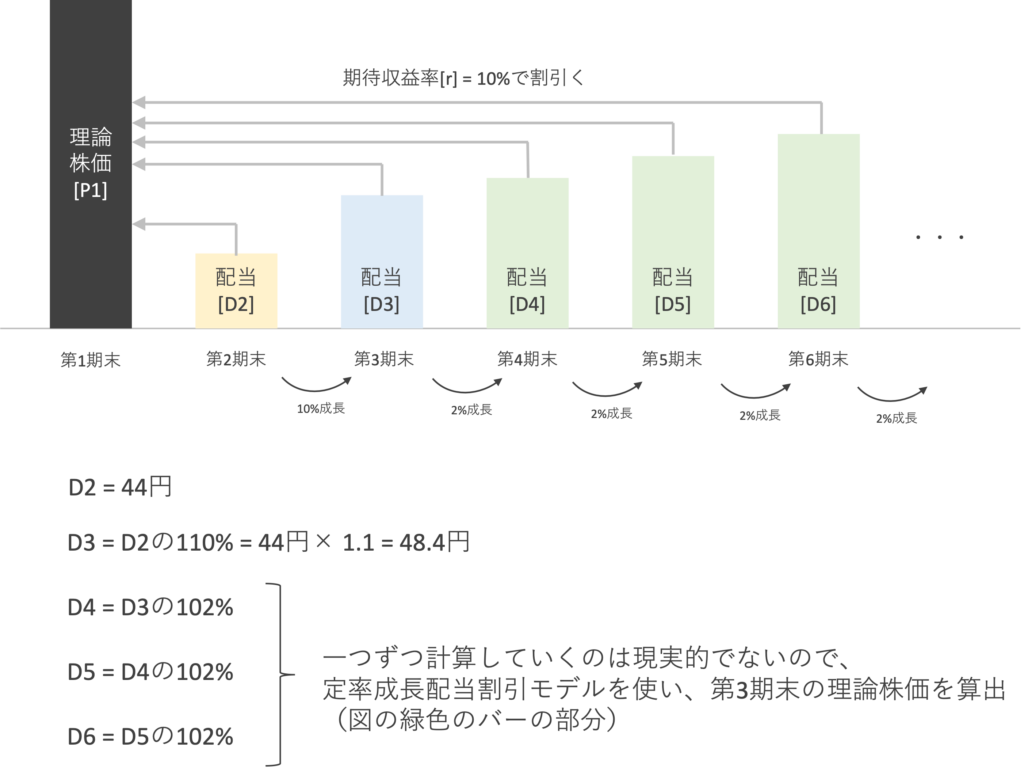
定率成長モデルの式は、以下の通り、第4期末の予想配当額[D4]を「期待収益率[r]から成長率[g]の差」を除した値になりますので、
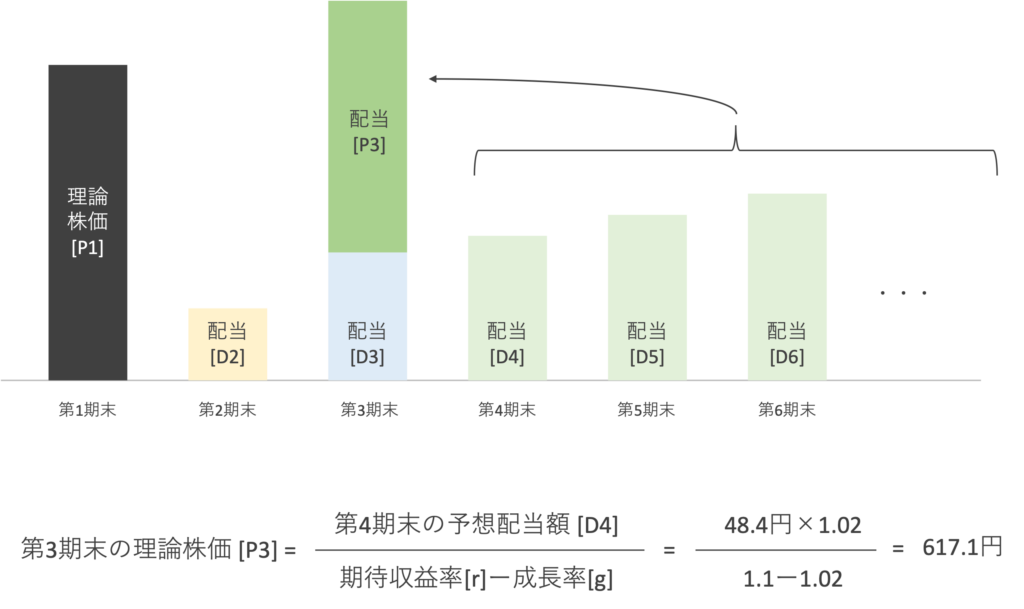
となり、P3は617.1円となります。
最後は、それぞれの期末の積み上げ額を期待収益率[r]=10%で割り引いたものを合算すると、
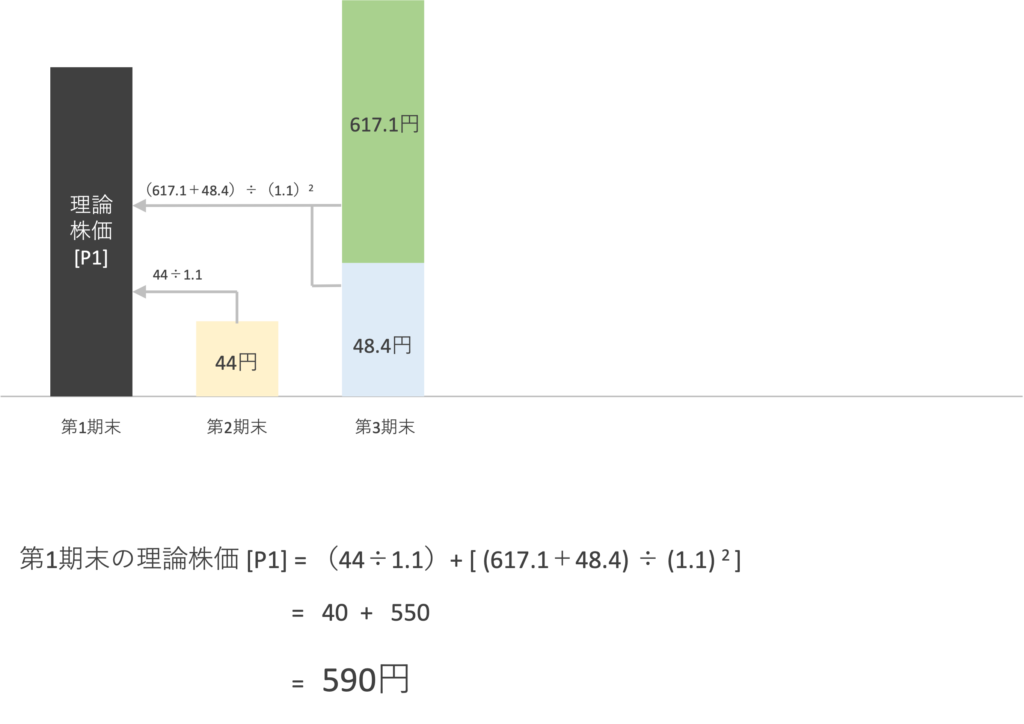
590円となります。
従い、答えは「イ 590円」です。
まとめ
ちょっと数式が多くて取っつきにくい記事になってしまいましたがいかがでしたでしょうか?
配当割引モデルや継続価値の計算は式さえ覚えていれば瞬殺できる問題が多いですが、ど忘れした時に備えて導出できる力を身につけておきたいですね。
それでは最後まで読んで頂きありがとうございました。












はじめまして診断士受験生の櫻井と申します。
色々とわかりやすい内容開示いただきありがとうございます。恐らくこちらの論点になるかと思っていますが財務会計
R3年第21問の解説を数列の和を使わず棒グラフなどの直感的な形で解法を記事にしていただければと思いますので一度ご検討だけでもお願いしたいと思います。本問の解説に関してはなかなか詳細かつ丁寧な解答記載のあるモノがなく困っております。
櫻井様
コメント頂きありがとうございました。ブログ継続の励みになりますので大変嬉しく存じます。
こちらの記事を更新する形で、解説加えましたので、ご確認ください!
tomatsu様 私の図々しいお願いにお付き合いいただきありがとうございました。昼食時間に連絡差し上げ、帰宅した今拝見して、あまりの早さに驚きと感謝の気持ちでいっぱいです。本当にご対応いただきありがとうございました。
櫻井様、
お役に立てていれば幸いです!改めましてコメントありがとうございました。他にも何かあればおっしゃってください!
すみません、一発合格道場の類似記事にもコメントしたのですがなかなか掲載されないのでこちらで重ねて質問させていただきます。
定率成長モデルで P – P(1+g)/(1+r) を計算する過程ですが、まずn年後までとすると、右辺には
-D1(1+g)^n-1/(1+r)^n
が残りますよね。
公比(1+g)/(1+r) = Rと置くと、これは
-D1*R^n/(1+g)
となります。企業が永続する、つまりnが無限大のとき、
lim(n→∞)D1*R^n/(1+g)は0に収束するから無視してよいということなのでしょうが、
それはRの絶対値が1未満の場合です。
今、rもgも正だと考えていますから、
(1+g)/(1+r) < 1、つまり g < r ということです。
これは配当金の成長率が期待収益率を上回ることはあり得ないことを意味しますが、
これはファイナンスの世界では常識や前提と捉えてよい話なんでしょうか?
文字に起こしてみるとそりゃそうか、とも思えるのですが、
数学的アプローチでここまでたどり着いたときに引っかかってしまいました。
ざいむがにがて様
ご連絡頂きありがとうございました。
また、道場にコメント頂いていたとのことですが、ご返信遅くなり申し訳ございませんでした(あいにく卒業していて通知がこない設定になっております。。)
頂いたご指摘、ごもっともでして、定率成長モデルが成立する条件は g < r が成立するときのみです。 本来、ブログ中の導出説明のなかで補足しておくべきでしたが便宜上割愛しておりました。混乱を招いてしまった場合は申し訳ございません。 なので、もし診断士試験で定率成長モデルを用いて計算をする場合、与えられている期待収益率が配当成長率よりも上回っていることを確認してから使用するのが「数学上」正しいと言えます。 (一方、診断士試験において配当成長率が期待収益率を上回るようないじわるな問題が出されることはないと思います)。 なお、ファイナンスの世界で配当成長率が期待収益率を上回ることはありえないのか?というご質問に対する個人見解ですが、ありえないことはないと思います。 というのもこれらの評価モデルはあくまでも「モデル」であって、どんな期待収益率を要求するかは投資家のスタンスによりますし、 配当成長率もあくまでも投資家自身が「仮定」した仮定値であり、どんな値を設定するかは投資家の自由だからです。 仮に投資家が自由に設定した仮定値において、g < rが成立しない場合は、定率成長モデルの式が使えなくなるというだけの問題かと思います。 また私自身、そもそも毎年一定の率で成長することを見込むこと自体に厳密な意義があるとは思えず、 クイックに現時点の株価が割高なのか割安なのかを確認するために活用可能なツールという風に考えて頂くのが良いのかなと思いました。 以上、直接的な回答になっていないかもしれませんが、お役に立っていれば幸いです。
丁寧にご解説いただきまして感謝申し上げます。
疑問が解決いたしました。
モデル、ツールとして割り切って考えるのがよさそうですね。
tomatsuさんのような的確な解説に恵まれると励みになります。
ハンドルネームを変えられる日が来るよう、勉強を続けてまいります。
ありがとうございました。
ざいむにがて様、
ご返信頂きありがとうございます!そのように仰っていただけてブロガー冥利につきます。
ご指摘頂いたポイントにお気づきなさった時点で相当財務お得意かと思いますので、もう改名されても良いかと思います笑
試験対策応援しております!
この問題ですが、どの解説を読んでも4期末の金額を求めてから2期の金額に戻してますが、3期末の金額(48.4)から定率成長が始まるので3期末の金額を0.08で割って2期末の現在価値にし、44を足して1.1で割ればいいかと思うのですが。実際答えも合いますし、計算もかなり楽になります。
たくや様、
コメントありがとうございます!おっしゃる通りそのやり方が一番効率良いですね。